음정이란 무엇인가 / 음정의 이해 / 음정의 개념 / 음정표
음악 이론을 공부할 때, 음정은 가장 기초적이면서 중요한 개념이다. 음정을 이해하고 계산하는 것은 음 사이의 관계나 화음 사이의 관계를 파악하는 데 필수적이다다. 음정은 두 음 사이의 상대적인 높이의 차이를 나타내며, 이는 두 음의 진동수 비율을 계산하여 구할 수 있다. 음정이란 무엇인가 / 음정의 이해 / 음정의 개념 / 음정표 에 대하여 본격적으로 알아보겠습니다.

음정이란 두 음 사이의 거리를 말한다. 영어에서는 ‘간격'을 뜻하는 interval이라는 용어를 쓴다. 소리에서 '거리'라는 개념으로 설명하기는 부적절하므로 좀 더 정확히 말한다면 두 음 사이의 상대적인 높이의 차이라고 할 수 있다. 음의 높이는 진동수(Hz)로 표시한다. 진동수가 클수록 높은 음이 되고, 진동수가 작을수록 낮은 음이 된다. 하지만 두 음의 진동수의 차이를 절대적인 값으로 계산하면 안되고, 상대적인 비율로 계산해야 된다.
예를 들어, A3(3옥타브 라)의 진동수는 220Hz이다. 한 옥타브 위에 있는 A4음(4옥타브 라)의 진동수는 440Hz 이다. 한 옥타브 더 위에 있는 A5(5옥타브 라)의 진동수는 880Hz이다. A3와 A4사이의 진동수의 차이는 220Hz이지만, A4와 A5사이의 진동수의 차이는 440Hz이다. 두 차이의 크기는 배가 되지만 우리는 이 두 음정을 모두 ‘1옥타브' 또는 완전8도라고 부른다.
두 음의 진동수는 수치적인 차이가 아니라 상대적인 차이이다. 두 음의 진동수의 비율에 따라서 음정을 구분한다. 한 옥타브의 음의 진동수는 두 배가 되고 두 음사이의 비율이 두 배가 되면 완전 8도가 된다.
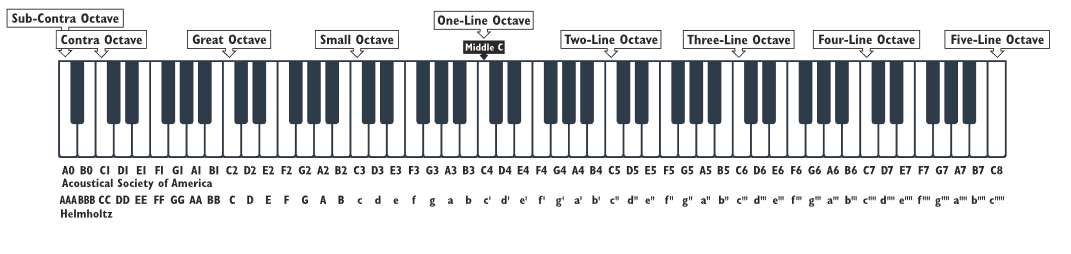
C Major Scale 을 기준으로 음정의 이름이 정해진다. C Major Scale은 피아노의 흰 건반만으로 이루어져 있기 때문에 기준으로 삼기에 좋다. C Major Scale은 첫 음을 낮은 C로 두고, 다른 한 음을 높은 음으로 두 음 사이의 간격에 따라 음정이 결정된다. 첫 음 끼리의 음정, 같은 음끼리의 음정을 1도라고 한다. 두 번째 음은 2도, 세 번째 음은 3도, . . . . 일곱 번 째음은 7도가 되는 것이다. 첫 음과 비교했을 때의 음정이다.

음정의 종류
C Major Scale 에서 8개의 음정을 기본음정으로 두고, 음정의 이름을 정하는 기준이 된다. 이 8개의 음정 앞에는 '완전(Perfect) 또는 '장'(Major)이라는 말이 붙는다. '완전'은 1, 4, 5, 8도 앞에 붙고, '장'은 2, 3, 6, 7도 앞에 붙는다. 같은 5도라고 할지라도 앞에 어떤 말이 붙느냐에 따라그 거리가 달라질 수 있다. C를 기준으로 5도가 되는 G와 Gb은 각각 완전5도와 감5도가 된다. 기준음정이 되는 완전 음정보다 반음이 좁기 때문에 왼쪽으로 이동하여 감5도가 되는 것이다. 이 개념은 음정표를 보면 보다 쉽게 이해할 수 있다.

기준음정을 기준으로 좁아지면 반음하나 차이마다 왼쪽으로 이동하고, 넓어지면 반음하나 차이마다 오른쪽으로 이동한다.
피아노 건반을 동시에 이용해서 보다 쉽게 이해할 수 있을 것이다. C Major Scale 에서 C와 G는 ‘완전 5도(Perfect)’이고, 그보다 거리가 좁혀진 Gb은 같은 5도이지만 ‘감 5도(Diminished)’가 된다.

여기서 추가적으로 C가 반음이 올라가서 C#이 되면 어떻게 될까? C#과 Gb은 거리가 더 좁혀졌기 때문에 ‘겹감 5도’가 되는 것이다. 1, 4, 5, 8도 음정은 기준음정이 ‘완전(Perferct)’가 되지만 2, 3, 6, 7도는 ‘장(Major)’에서부터 시작한다. C에서 E는 ‘장3도’가 되고 C에서 Eb은 ‘단3도(Minor)’가 된다. 반대로 거리가 넓어져도 방식은 똑같다.
C와 A는 '장6도'가 된다. 여기서 A가 반음 넓어져 A#이 된다면 '증6도(Augmeted)'가 되는 것이다. 추가적으로 C가 반음 내려가 Cb(B와 같은 음이 되지만)이 되면 거리는 더 넓어지기 때문에 '겹증6도(Double Augmeted)' 가 되는 것이다.
이런 방식으로 기준음정을 기준으로하고 음정표와 피아노 건반으로 그 거리의 좁아지고 넓어지는 차이를 계산하면 음정을 쉽게 계산할 수 있게 된다.
동영상 정보
: https://www.youtube.com/watch?v=xpgRRvhyf9A
실용음악 대학교에서 값비싼 등록금을 내야만, 배울수 있는 수준높은 강의들을 정말 말도 안되는 비용으로 시청하실수 있습니다. 클릭하여도 열리지 않는 영상은 회원전용 영상입니다. 회원가입후 시청하실수 있습니다.
가입버튼이 보이지 않은 경우는 유튜브에 로그인이 되지 않은 상태라 그렇습니다. 유튜브에 로그인을 하시면 가입버튼을 보실수 있습니다. 특히, 컴퓨터에서는 검색엔진을 크롬(구글)으로 실행하셔서 유튜브를 실행하셔야 됩니다. 크롬이 구글의 검색엔진이라 그렇습니다. 따라서 웹싸이트에 링크된 유튜브 영상들에서는 로그인 되지 않습니다.
취미로 음악을 즐기시는 분은 물론이고, 애드립, 작곡과 편곡에 관심이 있으신분, 실용음악대학교를 진학하려는 수험생, 또 현재 실용음악을 전공하시는 분들중에 이론에 정말 자신없는 분들께 자신있게 추천드립니다.
저도 음악이론을 처음접할때 이해도 안되고, 많이 힘들었습니다. 그러한 경험들을 바탕으로 만든 영상들입니다. 한영상당 3번정도 반복하시면 음악이론의 체계가 잡힐 것입니다.
2023.03.28 - [음악 관련 글] - 텐션(Tension)이란 무엇인가 / 7th Chord에서 사용할 수 있는 Tension
텐션(Tension)이란 무엇인가 / 7th Chord에서 사용할 수 있는 Tension
텐션(Tension)이란 무엇인가 / 7th Chord에서 사용할 수 있는 Tension 코드(Chords)를 더 확장하여 7th 코드위 3도씩 음을 더 쌓아 올리면 더욱 풍성한 코드를 만들 수 있다. Triad에 7음을 쌓아서 7th 코드를
worshipw.tistory.com
https://link.coupang.com/a/bpGt99
일산오빠의 실용음악 시창 청음:음정 코드 리듬 스케일 악기까지 강의+음원+연습을 모두 한 번에
COUPANG
www.coupang.com
"이 포스팅은 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다."
'음악 관련 글' 카테고리의 다른 글
| Diatonic 7th Chords 는 무엇일까? / 음의 진행 (0) | 2023.03.31 |
|---|---|
| 스케일(Scale) 이란 무엇인가 / 모드(Modes) / Relative Modes / Parallel Sacle (0) | 2023.03.29 |
| 텐션(Tension)이란 무엇인가 / 7th Chord에서 사용할 수 있는 Tension (0) | 2023.03.28 |
| 코드란 무엇인가 (2) / 7화음 / 7th Chords / Diatonic Triads / Sus4 (0) | 2023.03.28 |
| 코드란 무엇인가 (1) / 3화음 (장화음 / 단화음 / 감화음 / 증화음) (0) | 2023.03.28 |



